Boxing Pythagoras

On really, really, stupidly large numbers

When I was a kid and I got into an argument, inevitably it would devolve into a “Yuh-huh!” followed by a retort of “Nuh-uh!” After that, my brilliant counter argument would be “Yuh-huh, yuh-huh!” which was usually followed by “Nuh-uh, nuh-uh, nuh-uh!” It wouldn’t take us long to realize that repeating this, ad nauseum, would become irritating even to ourselves, so we soon came up with the idea of multiplying our answers: “Yuh-huh times ten!” would be followed by “Nuh-uh times a thousand!” But soon, we would reach the extent of big numbers that we could name. Most kids were familiar with “million,” “billion,” and even “trillion,” but numbers bigger than that often eluded us. Usually, after that, kids would either use nonsense words like “bajillion” or else they’d go back to repetition with “million million million.” However, occasionally, there were those few of us clever enough to learn about the bigger numbers. We’d learn “quadrillion” through “nonillion,” but the prefixes after that quickly became too confusing for little kid brains. Then we learned about a googol, 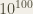, or (as we knew it) “a one followed by a hundred zeroes.” This number seemed insanely large, but remained easy (and fun!) for kids to say. Soon after learning about a googol, we would learn about the number googolplex, 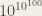or “a one followed by a googol zeroes.” This number was so large, most of us couldn’t truly comprehend it, but since it was easy to say, we kept on using it.

I’m an adult, now, and even though my style of persuasive argument has become just a bit more sophisticated than it once was, I still find myself fascinated with really, really large numbers. Today, I want to talk about one of my favorites, called Graham’s number. It is so ridiculously, stupidly large, that a googolplex is only negligibly larger than 1, when compared to Graham’s number. The number was invented by Robert Graham in the late 70’s to represent the largest possible solution (or “upper bound,” in math speak) to a particular mathematics problem. I’d love to just tell you what Graham’s number is, but there’s a problem. You see, Graham’s number is so large that the usual mathematical operations with which people are familiar are entirely inadequate to describe it. A billion can be easily explained as “a thousand times a thousand times a thousand,” and a googolplex can be understood as “10 to the 10 to the 100th power;” but Graham’s number is so inordinately big that even nesting exponents is fairly useless in describing it. So, I’ll begin our journey, today, by talking about Knuth’s up-arrow notation.

Read more…