Pi is Stupid
I teach Brazilian Jiu-Jitsu to people of all ages, from preschoolers to middle-aged parents. While BJJ, in itself, is not necessarily the most academic of pursuits, I also happen to be a huge nerd. So while teaching some of my 8 to 13 year-old students, it sometimes happens that I overhear them talking about their math classes, often to complain about ideas that they’re struggling to grasp. Being a huge nerd, and also a delighted teacher, I do my best to help them through these issues. If I can teach a kid how to find the length of the hypotenuse of a right triangle at the same time as teaching her how to finish a Triangle Choke, I become pretty much the proudest martial arts instructor you could hope to meet.
One of the things that my kids often use in their math classes, but almost never really understand, is the constant π (pi). They are taught π in class to help learn things like how to calculate the area of a circle, but they usually don’t really know what π actually is. They just think of it as some number that they have to memorize, never thinking about where the number comes from, or why it is what it is. Sometimes, I’ll tell the kids that they can earn their way out of doing push-ups if anyone can tell me what π is. Most often– after the jokes about desserts are made– I’ll hear someone say, “Coach, π is three-point-one-four!” Every now and again, one of the kids is clever enough to say, “Coach, π is three-point-one-four-on-into-infinity!” They get confused when I tell them that’s the value of π, but that is not what π actually is. It’s not their fault that they get confused by this; they were usually taught about π all wrong. I don’t even blame their math teachers, because most of the time, those math teachers were also taught about π in the wrong way. For a very long time, math classes have been teaching that π is a number, instead of teaching that π is the relationship between a circle’s circumference and its diameter. There is a reason it has been taught this way.
Ladies and gentlemen, π is just plain stupid.
Let me explain, for a moment. I don’t mean that the value of π is incorrect, and I don’t mean that π is not actually the ratio of a circle’s circumference to its diameter. What I mean is that thinking about circles in terms of π is counterintuitive. Even once they learn geometry, most people still don’t understand why we use π in our calculations; they simply know that we use it. The reason for this strange disconnect, in my opinion, is that mathematics describes circles by their radius in almost every single instance; except for the definition of π, where we instead look at the circle’s diameter. This is sort of like always measuring a racetrack in kilometers, except when it is a motorcycle track, in which case you measure in miles. Sure, you can convert miles to kilometers easily enough, but does it really make sense to do things this way?
The best way to explain what I mean will probably be to illustrate the issue. After all, circles are very visual things, and it can be difficult to really understand what I’m trying to say unless you can see it in front of you. So, let’s start by defining exactly what a circle actually is. A circle is the set of all points in a plane which are equidistant from a single origin. Look at the diagram, below. The curved, green line is our circle. At the center of the circle is point O, the origin point. Points A and B lie on the circle a distance r from the origin, just like every other point on the circle. We refer to this distance r as the radius.
Now, let’s pretend that we have a farmer who owns a small chunk of land. According to his deed, the farmer owns all the land within one mile of his farmhouse. As we can see by our definition, this means that the boundary of the farmer’s land is a circle with a 1 mile radius which has an origin point at the farmhouse. Now, the farmer needs to plan how much seed he will plant, and how to irrigate his new land; and in order to do that, the farmer needs to know exactly how much land he will actually be working. He needs to know the area of the circle.
If I presented this problem to my kids, they would joyfully exclaim, “Simple, coach! The area of a circle is !” Unfortunately, being the meanie that I am, I would then ask the kids, “But why is the area of a circle
?” Let’s pretend, for a moment, that our farmer has never seen the formula for the area of a circle, before. He can do some simple arithmetic, but he’s no mathematician. So, he decides to take this problem over to his friend, Archie, who happens to be a really well-renowned math scholar. He then asks Archie how to find out how much land his farm is going to cover.
Archie thinks about the problem for quite a while. It’s easy to find areas for shapes which are bounded by straight lines, like triangles and rectangles, but circles are very difficult. So Archie decides he wants to compare the area of the circle to one of these easier areas. He draws the following picture, and asks a simple question: does the right triangle have a smaller area than the circle, a bigger area, or the same area?
Let’s call the area of the circle and the area of the triangle
. Now, Archie still doesn’t know how to find
, but he knows that the area of a triangle is
where
is the length of the triangle’s base and
is its height– because a triangle is half of a rectangle, and a rectangle’s area is its length times its height. So that means our triangle, in Figure 2, has an area of
. Now, here’s where he gets really clever. Archie draws a triangle inside the circle, with one vertex at the origin and two on the circle itself. If he copies this triangle, rotating the copies inside the circle, he can make a new shape called a polygon. And since he can calculate the area of each of those little triangles, he can calculate the area of that whole polygon,
, and compare it to
. If the area of the right triangle,
, is less than the area of the circle,
, then we should be able to make a polygon inside the circle which has an area equal to
.
The area of this polygon is given by the formula where
is the number of triangles. However, multiplying the base length of each triangle,
, by the number of triangles,
, simply gives us the perimeter of the polygon,
. This means that our formula becomes
. We can see, in Figure 3, that no matter how many triangles we make inside the circle, the perimeter of our polygon will be smaller than the circumference of the circle (
) and the height of the triangles will be less than the radius of the circle (
), so we can conclude that
. No matter how many sides the polygon has, its area will still be smaller than
. It is impossible to create a polygon inside the circle which has an area equal to our right triangle. This means that the right triangle from Figure 2 cannot possibly have a smaller area than the circle.
Is it possible, then, that is greater than
? We can perform another experiment with triangles in order to find out. Let’s say we make an isosceles triangle with height
which has one vertex at the origin of the circle and two vertices which lie outside the circle, such that the base of the triangle is tangent to the circle at its midpoint. We can similarly rotate this triangle about the origin to form another polygon. If the area of the right triangle is bigger than the area of the circle, then we should be able to create a polygon surrounding the circle which has an area equal to
. Again, we know that
; but in this case, we know that the perimeter will always be larger than the circumference (
) and that the height is equal to the radius (
). Therefore, we know that
, no matter how many triangles we use to construct the polygon. It is impossible to create a polygon surrounding the circle with an area equal to our right triangle. This means that the right triangle from Figure 2 cannot possibly have a bigger area than the circle.
So, now we have determined that cannot be smaller than the area of the circle, nor can
be larger than
. Therefore, we must conclude that
; that is to say, the area of a circle with radius
and circumference
is equal to the area of a right triangle with legs of length
and
. So, that means that
. Of course, we still have a problem: we don’t know the value of
, nor a method for calculating it.
Now, you’re probably saying to yourself, “That’s great, but what the heck does any of this have to do with π?!” Well, our Archie was actually Archimedes of Syracuse, an extremely smart mathematician. He recognized this problem with calculating the circumference, as well, and he actually discovered a pretty brilliant method to help solve the problem, too, using inscribed and circumscribed polygons, like the ones from Figures 3 & 4. Unfortunately, when he formulated his conclusion, Archie stated, “The ratio of the circumference of any circle to its diameter is less than but greater than
.” This was the first rigorous attempt to calculate π in mathematics history, but did you notice the switch? Throughout this entire discussion, we defined and described the circle entirely by its radius. However, when we finally got to the conclusion, Archimedes decided to put it in terms of the diameter– which is 2 times the radius! We can speculate any number of reasons why Archie might have done this, but the unfortunate fact of the matter is that mathematicians spent the next 2000 years following his lead. Circle functions were always described by the ratio of the circle’s circumference to its diameter, even though the radius is a much more natural value for comparison. Every time you use π in an equation, that equation has to account for the conversion between radius and diameter. This is a terrible and fundamental mistake which has been making mathematics more difficult for an extremely long time.
But don’t worry, friends. There is a better way!
What if we decided to define our circle constant by the radius instead of the diameter? Let’s call the ratio of a circle’s circumference to its radius τ (tau), since it represents one full turn (Greek, τορνος) of a circle. Way back in the beginning of this article, we asked why the area of a circle is . Even after all the work we’ve done, it still might not be readily apparent. So, let’s switch tack and look at τ, instead. What if I told you that the formula for the area of a circle is
? Suddenly, it’s much easier to see why this is true. We already proved that
. We have defined our new circle constant as
, but if we solve this equation for
we find that
. Plugging this back into our area formula, we get
! It’s really easy to see why the area formula is what it is, using τ; as opposed to using π, where it gets totally obfuscated.
So, let’s look at a few areas where τ is superior to π…
Circumference of a Circle
versus
When we use τ in the formula for the circumference of a circle, we show a simple, direct relationship between the circumference of the circle and its primary property, the radius. On the other hand, when using π, we either have to define in terms of diameter, which is a property of circles that is almost never utilized in mathematical formulae, or we have to add a second corrective constant to our equation, the number 2, in order to convert π into a useful value. Why not just employ a useful value, to start with, instead of a stupid one?
Area of a Circle
versus
At first glance, some people might think π is the better choice, here, since the final equation is simpler. However, as we showed in the main article above, this actually makes it more difficult for people to understand why the area formula is as it is. It becomes a matter of memorization, rather than one of actual comprehension. This would not be so bad if this was the only equation where this was the case, but unfortunately the area formula sets a precedent of memorization-over-understanding which is then inherited by almost every other formula involving circles– and there are a lot of other formulae which involve circles. The use of τ resolves this problem by reminding the student that a circle has the same area as a right triangle with legs of length and
. Less memorization makes for smarter students.
Angular Measurement
Do you remember how confusing it was to have to memorize all those angles in radians? When you couldn’t remember what angle was supposed to be representing, you’d convert it back to degrees, first, then you knew that 120° is a bit more obtuse than a right angle. So weird! But, if you use, τ you see that the angle is
, which is just one third of a circle.
Look at the image, above. Using τ makes angular measurement so simple! You don’t have to worry about dividing the circle up into 360 degrees– an archaic legacy of ancient Babylonian mathematics which still persists, today, for some stupid reason– nor do you have to memorize the strange formulations with π that constantly confuse trigonometry students. Want to know the angular measurement of an eighth of a circle? That’s just . Looking at a right angle? Well, a right angle is just a quarter of a circle–
. Trying to figure out what angle
radians represents? Well, that’s just
of a circle! It is immediately obvious that τ is superior to both π and degrees of angle, when one looks at Figure 5.
Trigonometry
Look at how much more naturally τ measures the Sine wave than does π! Just like we saw in the angular measurement, above, it is much easier to discuss the period of trigonometric waves in terms of τ, which makes these things far easier for teachers to teach and for students to understand. The sine wave measures properties of a unit circle. The maximum value of is the radius
, and the period of the wave is the circumference
. This makes far more sense when we are using a circle constant which is directly in terms of
and
, like τ, than one which is in terms of
and
, like π.
Numerically
versus
As we can very easily see, , therefore τ is greater than π. ‘Nuff said!
Conclusion
More than two thousand years ago, a brilliant mathematician made a dumb mistake when he was trying to figure out some of the crazy aspects of circles. Unfortunately, almost every mathematician that followed him just figured they’d follow his lead, without thinking that there might be a better way to talk about circles. It wasn’t until relatively recently that a small handful of people began to realize just how stupid π actually is. Back in 2001, mathematician Bob Palais published an article in The Mathematical Intelligencer called Pi is Wrong! in an attempt to bring this issue to light. Some time later, physicist Michael Hartl published his Tau Manifesto, which became an internet sensation and really began the movement which eventually showed me the error of Archie’s ways (and which was the source for the images in Figures 5 & 6). If you want to see an in-depth look at even more ways in which τ is superior to π, I definitely recommend Hartl’s page. Since the publication of the Tau Manifesto, the case for τ has been picked up by educators, students, and general nerds all over the world, and while our effort is still slow going, we have definitely made some progress in alerting people to the fact that π is stupid.






If they really wanted it to catch on, they’d name it Cak. But that’s its own debate.
The tau vs pi discussion is an interesting one because it’s good that we question long held conventions in any field and though there are merits of tau, some of which you have listed I am unconvinced that it’s worth abandoning the historical convention. Every argument for one can be reversed to the other, ‘the circumference of unit circle is ‘ (oh well the sum of angles in a a triangle is
‘ (oh well the sum of angles in a a triangle is  , the period of
, the period of  and
and  is
is  (oh well the distance between their zeros is
(oh well the distance between their zeros is  and so is the period of
and so is the period of  ), ‘the whole turn is more natural than the half turn’ (oh well when measuring latitude on a sphere only half turns are actually meaningful and do we not live on a sphere?(sort of)), and so on and so on.
), ‘the whole turn is more natural than the half turn’ (oh well when measuring latitude on a sphere only half turns are actually meaningful and do we not live on a sphere?(sort of)), and so on and so on.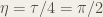 and you could form a just as convincing argument for that if you wanted to.
and you could form a just as convincing argument for that if you wanted to.
It’s all arbitrary and looking at history the Greeks really (seem to have) thought of angles as relative straight angles
We could make a switch to any of the three and nothing would change so I wouldn’t be all upset if edu policy did the shift but I’m voting for continued use of since it’s the way that requires the least work all things considered.
since it’s the way that requires the least work all things considered.
Thank you for your input! I apologize that LaTeX seems to be screwing up in the comments section– I’ll see if there’s anything I can do to fix that, on my own, but it may be an issue with either my theme or with WordPress.
I completely agree that whatever base unit we choose for the circle constant is arbitrary, and that they all are ultimately mathematically sound; but my argument is that some arbitrary choices are better than others, regardless of their being equivalently sound. In my opinion, the most basal arbitrary choice is the best one. And, when it comes to circles, the most basal choice is a ratio of circumference to radius, the whole path carved out by the circle to the basic property which defines that circle.
Let’s look at the “sum of angles in a triangle” argument, for a moment. Yes, the sum of the angles in a triangle is π radians. But what is an angle? Well, an angle is the measure of rotational relation between two line segments which share a vertex. How do we measure that rotation? In comparison to a circle. The angle is the ratio of the arc distance– that is, the length traveled along the circumference– to the radius of a circle. An angle, therefore, is some division of τ.
For the “intervals between the zeroes of sine/cosine,” we need to ask what sine and cosine are actually doing. The quick answer to this question is that sine and cosine are functions for determining properties of angles. This, of course, leads us back to the question, “What is an angle?” which we answered above.
For the “half turns on a sphere” argument, we ask, “What is a half turn?” Well, a half turn is an angle measuring half the arc of a circle. What is an angle?
Et cetera, et cetera.
Which option for the circle constant makes the most sense? Do we go with the Babylonians, who used C/(360r)? Or with Archimedes, who used C/(2r)? Or do we just get rid of unnecessary coefficients and use τ?
I think whenever someone argues that a thing is natural it is just an expression of that persons aesthetic preferences rather than there being anything substantial about it. I find the half turn to be more pleasing as a unit because it is something while the whole turn is really nothing at all.
Still, the only real argument for tau is if the overall burden of learning math is reduced by the shift and I’m not convinced that tau would serve that purpose to the degree some supposes as any ‘factor two’-related difficulties you might have have more to do with having problems understanding and working with fractions and you should treat that ‘disease’ directly instead of the symptoms.
Thanks, again, for reading and replying!
When I say ‘natural’ or ‘basal,’ I’m not attempting to invoke any aesthetic value of a particular choice. Rather, I am attempting to describe the amount of information which is required to define that choice. So when I say “a more natural option,” I mean that this option requires less information in its definition. While it is true that I find such basal approaches more aesthetically pleasing, as well, it is not the aesthetics which drive my argument.
If one could provide a definition for an angle which is more basal in terms of a half turn than it is in terms of a full turn, I would gladly support π over τ. However, it would seem that the definition of a half turn is predicated upon the definition of a full turn, and therefore any definition for “angle” based on the half turn would require more information than one based on the full turn. This is why I argue that τ is more natural than π.
Any time we reduce the necessary information to define a topic, we reduce the overall burden of learning as a consequence. The “disease” you refer to when talking about difficulties with the 2-factor on the π system is a lack of geometric intuition. That lack of geometric intuition is caused by the fact that formulae for properties of circles are taught through memorization more often than through derivation or proof. This memorization didactic is due to the fact that simplifying equations with an extraneous 2-factor often obfuscates the derivation– as I demonstrated in my post with A=πr^2– making it harder for a student to trace backward from a formula to its derivation. Even if we don’t replace π with τ, it would be worthwhile to replace πr^2 with (1/2)Cr.
But then using tau makes a kludge of Euler’s Identity e^(i*t/2)+1=0 so it’s a matter of pick your poison.
Thanks for reading!
Honestly, I rather think that Euler– had he utilized τ over π– would have constructed his eponymous identity in terms of τ. In which case, he would have resolved e^(iθ) = cos θ + i sin θ into the simple identity e^(iτ) = 1.
Awesome.
You’ve convinced me that A = (1/2)Cr is better than A= πr^2.
What happens when derivatives and integration are done using tau instead of pi? If degrees are used, (sin∘)′=(π/180)cos∘. Would using tau require multiplying or dividing by 2 depending on the operation done?
Great question!
Whether we are using τ or π, we are still measuring our angle in radians, the unit of measure for which the trig functions are defined. The problem with derivatives or integrals over trig functions measured in degrees of arc is that this unit of measure includes a hidden conversion factor which must be taken into account for the Chain Rule.
For example, let’s say we’re looking to find the derivative of sin(45°). The problem is that 45° is actually just a shorthand method of writing that we’ve gone 45/360 of the way around the circle’s whole arc. When we apply the Chain Rule during the derivative, this hidden factor becomes very important. Incidentally, even though it’s not used too often these days, the Gradian unit of measure suffers from a similar issue, since (for example) 50 gradians is actually shorthand for 50/400 of the way around the circle’s whole arc.
The difference when using τ or π is that the conversion factor is not hidden. We are already measuring in radians. All of the factors necessary for the Chain Rule are already right in front of us. So, when we are looking at, say, π/4 radians, there is no conversion factor necessary. We already mean π/4 of the whole arc of the circle. Similarly, when we are looking at τ/8 radians, we already mean τ/8 of the whole arc. In both cases, we are already measuring by the fundamental unit utilized by the definitions of the trigonometric functions.
Hope that helps!
Thank you for your thoughtful answer. Clearly if tau had been used all along, nobody would be making any effort to get people to start using pi.
I have an amusing question to pose…If I have a whole Pi and I remove one Plank, is there still enough Pi to go round?