Egyptian Math: Multiplication and Division
A little while back, I wrote up a little post on basic Egyptian mathematics, concentrating on how using Egyptian numerals in addition and subtraction can aid students in understanding our base-10 number system. I wanted to continue that discussion, today, by looking at how the ancient Egyptians performed Multiplication and Division. Unlike my discussions of addition and subtraction, I am not advocating Egyptian multiplication and division as a means for teaching the Common Core standards.
To be honest, I just find the system to be really interesting.
Figure 1: Egyptian numerals
As a brief reminder, the symbols in Figure 1 represent the Egyptian numerals. If a person wanted to write a number larger than 1 but less than 10, they would use multiples of the 1-numeral to represent it. For example, ‘three’ would be written as |||, while ‘five’ would be recorded as |||||. The same goes for the larger numeral symbols, so a number like ‘thirty-four’ could be written ∩∩∩||||, et cetera.
We saw precisely how easy addition can be, on this system, in the previous post. However, the way in which we were taught multiplication and division is so thoroughly entrenched in the Indian-Arabic numeral system, it can be very difficult to see how to perform such operations with different symbols. Let’s break down these operations, as if we were learning them for the first time, in order to find out how we might go about this work. What does it mean to multiply 3 by 5? Well, it means that we have five groups, and each group consists of three things. The total number in all of the groups is the solution to our question; that is, 
Figure 2: Five groups of Three
Once we have written out these five groups of three, all that remains is to count them all up for a total. Just as in the previous article, when we count up ten of the 1’s numeral, we scratch them off and replace them with a 10’s numeral. The remaining symbols are our solutions.
Figure 3: Five groups of Three is Fifteen
This would seem simple enough for multiplication of relatively small numbers. However, it is immediately apparent that this process would very quickly become unwieldy when applied to larger numbers. Lots and lots of groups with a great deal more numerals would make the final counting process extremely painstaking and tedious. For example, what if we wanted to multiply 587 by 24?
Figure 4: Twenty-four groups of 587
Obviously, this would make mathematics particularly tedious, incredibly difficult to read, and extremely prone to simple counting mistakes. So, the Egyptians developed an ingenious method for simplifying multiplication based upon a process of Doubling. While it is a painstaking process to count up numerous groups of large Egyptian numbers, it is a fairly trivial task to double any particular Egyptian number– just add the number to itself using regular addition methods. The ancient mathematicians of Egypt discovered that they could use a method involving repeated doubling to solve these difficult multiplication problems. Let’s take a look at how they would have tackled the problem of 
Figure 5: Egyptian multiplication
The image in Figure 5 might look a bit confusing, at first, so let’s break down the process a bit. We’ve constructed a table. The left-hand column of the table represents numbers of groups. At the top of the column is a target number, the total number of groups we wish to calculate. The right-side of the column indicates the total value of those groups. So, reading the table, we see that one group of 587 has a value of 587, two groups have a value of 1174, four groups have a value of 2348, et cetera. If we want to know the value of twenty-four groups of 587, we only need to add together the values of enough groups. Since eight groups added to sixteen groups gives us twenty-four groups, adding the values from these rows will lead us to the value of twenty-four groups: 14,088.
Let’s try another problem. This time, for the sake of readability, I will forego the use of Egyptian numerals. The method remains exactly the same, despite our more familiar Indian-Arabic numeral system. So, this time, let’s calculate 
Figure 6: 3256×233
The Egyptian system of multiplication was a fairly ingenious method for simplifying a process which was otherwise complex. It was quite likely the best possible algorithm that their numeral system could afford, and it was more than capable of yielding the solutions necessary to Egyptian scholars. However, the most brilliant aspect of this method might have been the fact that, by only slight alteration, it could just as easily be utilized for calculating Division as for Multiplication. For example, let’s say that instead of 
Figure 7: 3256÷233
This time, our target number is not the total number of groups which we desire to calculate, but rather the total value of those groups, so we place it atop the right-hand column. Then, as before, we begin with one group of 233, and proceed to repeatedly double. We then mark off all of the rows which, when added, bring us as close to our target number as possible without exceeding it. Adding the number of groups from these rows gives us our quotient, while subtracting the total of these rows from our target number yields our remainder. This leads us to an interesting pedagogical benefit of the Egyptian system of multiplication and division. Unlike our current methods, in which multiplication and long-division are very different algorithms, the same process utilized for Egyptian multiplication also performs division. Students only had to learn the one method in order to understand both.
The scholars of ancient Egypt did not have the benefit of the shortcuts implicit to the Indian-Arabic numerals which we now utilize. However, they discovered some incredibly efficient methods for calculating products and quotients, nonetheless. It is absolutely fascinating that, even 5000 years ago, humanity was able to combine patterns of patterns in this sort of algorithmic process. It certainly causes one to appreciate the education and skill which went into the historical development of mathematics.
Boxing Pythagoras 
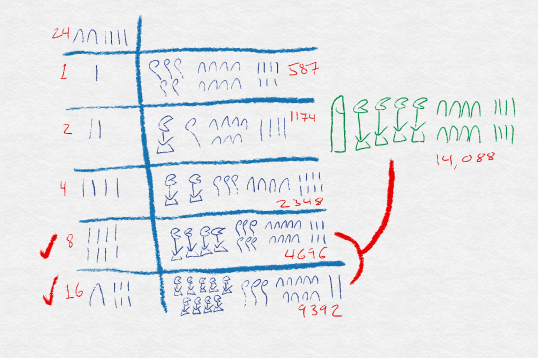
I’ve always liked the Egyptian multiplication and division system; it starts out looking like it’s some ridiculously overcomplicated thing, but then, when you get done with the problem it feels almost like you just saw a magic trick. “And the number you were trying to compute was … 2038!”
Hi great readinng your post